Demystifying the Black-Scholes Option Pricing Model: A Comprehensive Guide

In the world of finance, options play a vital role in managing risks and maximizing returns. One of the most influential models used for pricing options is the Black-Scholes model. Developed by economists Fischer Black and Myron Scholes in 1973, this groundbreaking model revolutionized the field of quantitative finance. By providing a mathematical framework for option valuation, the Black-Scholes model transformed the way investors and traders approach the derivatives market.

 

This comprehensive guide aims to demystify the Black-Scholes option pricing model, breaking down its key components and assumptions. We will explore the underlying principles and equations that form the foundation of the model, discuss the significance of its assumptions, and illustrate its practical applications. Whether you're an aspiring quantitative analyst, a finance enthusiast, or simply curious about option pricing, this blog will equip you with a deeper understanding of the Black-Scholes model.

 

1. Understanding Options : 

 

Before delving into the Black-Scholes model, it is essential to grasp the concept of options. An option is a financial derivative that gives the holder the right, but not the obligation, to buy (call option) or sell (put option) an underlying asset at a predetermined price (strike price) within a specified time period (expiration date). Options provide flexibility and risk management opportunities to investors, as they can hedge against adverse price movements or speculate on future price changes.

 

2. The Black-Scholes Model Assumptions: 

 

The Black-Scholes model is built upon a set of assumptions that simplify the complex reality of financial markets. Understanding these assumptions is crucial for comprehending the model's strengths and limitations. The main assumptions of the Black-Scholes model include:

 

• Efficient markets: The model assumes that financial markets are efficient, meaning there are no arbitrage opportunities, and prices follow a random walk.

 

• Constant volatility: It assumes that the volatility of the underlying asset's returns remains constant throughout the option's life. This assumption is known as the constant volatility assumption.

 

• Log-normal distribution: The model assumes that the returns of the underlying asset follow a log-normal distribution. This assumption simplifies the mathematical calculations involved in the model.

 

• No transaction costs: The model disregards transaction costs, such as brokerage fees and taxes, to simplify the analysis.

 

• No dividends: It assumes that the underlying asset does not pay dividends during the option's life.

 

Also Read | FinOps: The Cloud Financial Management Practice

 

3. The Black-Scholes Equation:

 

The Black-Scholes model provides a partial differential equation known as the Black-Scholes equation, which calculates the theoretical price of a European call or put option. The equation combines several variables, including the current price of the underlying asset, the strike price, time to expiration, risk-free interest rate, and volatility. The Black-Scholes equation is as follows:

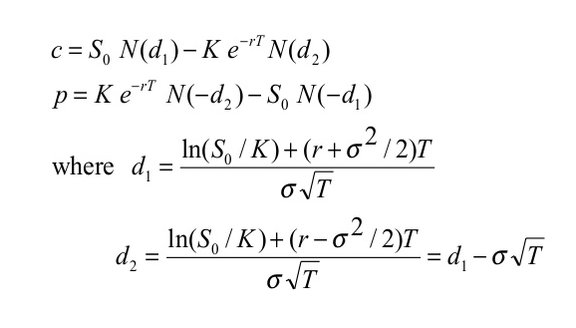
Where:

C: Call option price

S: Current price of the underlying asset

K: Strike price of the option

r: Risk-free interest rate

T: Time to expiration

σ: Volatility of the underlying asset

 

The Black-Scholes equation is derived using a combination of advanced mathematical techniques, including stochastic calculus and the concept of risk-neutral pricing. The solution to the equation provides the theoretical fair value of the option at a specific point in time.

 

4. Option Greeks:

 

To gain a comprehensive understanding of option pricing, it is crucial to grasp the concept of option Greeks. Option Greeks are measures that quantify the sensitivity of option prices to changes in various factors. The Black-Scholes model introduced several option Greeks that help investors assess the risk and potential profitability of options.

 

These Greeks include:

 

a. Delta (Δ): Delta measures the change in the option price relative to changes in the underlying asset's price. It indicates the sensitivity of the option's value to movements in the underlying asset. Delta ranges from 0 to 1 for call options and -1 to 0 for put options. A delta of 0.5 means that for every $1 change in the underlying asset's price, the option price will change by $0.50.

 

b. Gamma (Γ): Gamma measures the rate of change of delta. It gauges the acceleration or deceleration of delta as the underlying asset's price moves. High gamma values indicate that delta can change significantly with small movements in the underlying asset's price.

 

c. Theta (Θ): Theta measures the rate of time decay of an option. It quantifies how much the option's value will decline over time due to the passage of time alone. Theta is particularly important for options approaching their expiration date.

 

d. Vega (ν): Vega measures the sensitivity of the option price to changes in volatility. It indicates the impact of volatility fluctuations on the option's value. Higher vega values suggest that the option price will be more responsive to changes in volatility.

 

e. Rho (ρ): Rho measures the sensitivity of the option price to changes in the risk-free interest rate. It quantifies the impact of interest rate fluctuations on the option's value. Rho is more relevant for longer-term options.

 

Understanding these option Greeks allows traders and investors to make informed decisions regarding option strategies, risk management, and hedging techniques.

 

Also Read | Top 10 Financial Management Practices in 2023

 

Practical Applications

 

The Black-Scholes model has numerous practical applications in the financial industry. Some key applications include:

 

a. Option pricing: The model's primary application is determining the theoretical fair value of options. By inputting the necessary variables into the Black-Scholes equation, investors can calculate the appropriate price for a given option, enabling them to make informed investment decisions.

 

b. Risk management: The model facilitates risk management by allowing market participants to assess the risk exposure of their option positions. Option Greeks help quantify the potential risks associated with changes in underlying asset prices, volatility, time, and interest rates.

 

c. Option trading strategies: Traders often employ the Black-Scholes model to design and implement various option trading strategies. By analyzing different combinations of options and underlying assets, traders can identify opportunities for profit and hedge against potential losses.

 

d. Volatility forecasting: The Black-Scholes model's assumption of constant volatility can be used inversely to estimate implied volatility. By inputting market prices of options and reverse-engineering the model, implied volatility levels can be extracted, providing insights into market expectations.

 

e. Option valuation adjustments: The Black-Scholes model serves as a foundation for more complex models that incorporate additional factors and adjustments. These models account for market frictions, such as transaction costs, dividends, and non-constant volatility, to provide more accurate valuations.

 

Also Read | Financial Frauds: Types and How to Protect yourself against it?

 

Criticisms and Limitations

 

Despite its significant contributions to option pricing, the Black-Scholes model is not without its criticisms and limitations. Here, we will explore some of the common critiques of the model, shedding light on its shortcomings and areas where it may fall short in capturing certain market phenomena.

 

Assumptions: 

 

The Black-Scholes model relies on several assumptions that simplify the complexities of real-world financial markets. However, these assumptions can be unrealistic and limit the model's accuracy in certain scenarios. For example:

a. Efficient Markets: The assumption of efficient markets, where there are no arbitrage opportunities, may not hold true in all cases. Market frictions, such as transaction costs and liquidity constraints, can impact option prices and deviate from the model's predictions.

 

b. Constant Volatility: The model assumes that volatility remains constant over the life of the option. In reality, volatility can be dynamic and exhibit time-varying patterns. The constant volatility assumption may not accurately capture the volatility smile or skew observed in market prices.

 

c. No Dividends: The Black-Scholes model assumes that the underlying asset does not pay dividends during the option's life. This assumption may not hold for stocks or other assets that do pay dividends, leading to deviations between model prices and market prices.

 

Market Inefficiencies

 

The Black-Scholes model assumes that markets are efficient, meaning that prices follow a random walk and all available information is incorporated into the prices. However, real markets may exhibit inefficiencies, such as pricing anomalies or deviations from expected behavior. These inefficiencies can introduce discrepancies between model prices and observed market prices.

 

1. Skewed and Fat-Tailed Distributions: 

 

The log-normal distribution assumption of returns in the Black-Scholes model may not accurately capture the distributional characteristics of some underlying assets. Many market returns exhibit skewness (asymmetric probability distribution) and fat-tailed behavior (higher likelihood of extreme price movements). The model's reliance on the log-normal distribution can result in underestimating the probability of extreme events.

 

2. Transaction Costs and Liquidity: 

 

The Black-Scholes model does not account for transaction costs, such as brokerage fees and taxes, which can have a significant impact on trading strategies. Additionally, the model assumes perfect liquidity, meaning that it is always possible to enter or exit a position at the prevailing market prices. In reality, liquidity constraints can affect the execution and pricing of options.

 

3. Behavioral Factors: 

 

The Black-Scholes model assumes rational behavior and does not consider psychological biases or market sentiment. Human emotions and irrational behavior can influence option prices, leading to deviations from the model's predictions. Market events driven by fear, uncertainty, or herding behavior may not be captured by the model.

 

 

• Non-Stationarity and Time-Varying Parameters: 

 

Financial markets are dynamic, and the relationships between variables may change over time. The Black-Scholes model assumes stationarity and constant parameters, disregarding potential shifts in market conditions or regime changes.

 

American-Style Options

 

The Black-Scholes model is specifically designed for European-style options, which can only be exercised at expiration. American-style options, on the other hand, can be exercised at any time before expiration. The model's assumption of no early exercise may result in inaccuracies when pricing American-style options.

 

It is important to recognize these criticisms and limitations of the Black-Scholes model. While the model provides valuable insights into option pricing, it is essential to consider its assumptions and be mindful of the potential deviations from real-world market behavior. Researchers and practitioners have developed alternative models and extensions to address some of these limitations and provide more robust frameworks for option

 

Also Read | Best Financial Management Tips for your Enterprise in 2023

 

Conclusion

 

The Black-Scholes option pricing model has transformed the world of finance, offering a systematic and quantitative approach to option valuation. By understanding the key components, assumptions, and practical applications of the model, investors and traders can make more informed decisions in the complex derivatives market. However, it is essential to acknowledge the model's limitations and consider real-world factors that may deviate from its assumptions.

 

As financial markets evolve, alternative models and extensions of the Black-Scholes model continue to be developed, incorporating more realistic assumptions and addressing limitations. Nonetheless, the Black-Scholes model remains a fundamental tool in option pricing and has laid the groundwork for further advancements in quantitative finance.

 

It is worth noting that the Black-Scholes model is most applicable to European-style options, which can only be exercised at expiration. For American-style options that allow early exercise, additional considerations and techniques are required to accurately price them.

 

In conclusion, the Black-Scholes option pricing model revolutionized the field of quantitative finance by providing a mathematical framework for valuing options. Its assumptions, including efficient markets, constant volatility, log-normal distribution, no transaction costs, and no dividends, simplify the complexities of the financial markets. By utilizing the Black-Scholes equation and understanding the option Greeks, investors can analyze options, manage risks, and develop trading strategies.

 

However, it is essential to recognize the limitations of the model, such as the assumption of constant volatility and the disregard for transaction costs and dividends. Real-world market conditions may deviate from these assumptions, leading to discrepancies between theoretical prices and actual market prices. Thus, it is crucial to combine the insights from the Black-Scholes model with market experience, judgment, and consideration of other factors to make well-informed investment decisions.

 

As the field of quantitative finance continues to evolve, researchers and practitioners are constantly refining and enhancing option pricing models to better capture the complexities of financial markets. By staying updated with advancements in option pricing and understanding the underlying principles, investors can navigate the world of options with greater confidence and effectiveness.