How Does Linear And Logistic Regression Work In Machine Learning?

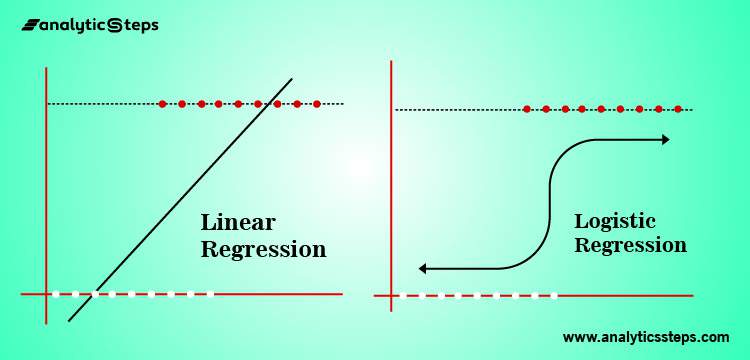
Linear regression and logistic regression both are machine learning algorithms that are part of supervised learning models. Since both are part of a supervised model so they make use of labeled data for making predictions. 

 

Linear regression is used for regression or to predict continuous values whereas logistic regression can be used both in classification and regression problems but it is widely used as a classification algorithm. Regression models aim to project value based on independent features.

 

The main difference that makes both different from each other is when the dependent variables are binary logistic regression is considered and when dependent variables are continuous then linear regression is used.

 

Linear Regression

 

Every person must have come across linear models when they were at school. Mathematics taught us about linear models. It is the same model that is used widely in predictive analysis now. It majorly tells about the relationship between a target that is a dependent variable and predictors using a straight line. Linear regression is basically of two types that are Simple Linear Regression and Multiple Linear Regression.

 

---

                                                             Experience on X-axis & Salary on Y-axis

---

In the above plot, Salary is the dependent variable that is on (Y-axis) and the independent variable is on X-axis that is Experience. More experience means more salary. The regression line can be written as:

 

 Y1 = a0 + a1X + ε

 

Where coefficients are a0 and a1 and the error term is ε.

 

Linear regression can have independent variables that are continuous or may be discrete in nature but have continuous dependent variables. The best fit line in linear regression is calculated using mean squared error that finds out the relationship between dependent that is Y and independent that is X. There is always a linear relationship that is present between both the two. 

 

Linear regression only has one independent variable whereas in multiple regression there can be more than one independent variable.

 

Let us go through a regression problem. We will use the Boston dataset from Scikit-learn, this dataset holds information about the house value of different houses in Boston. Other variables that are present in the dataset are Crime, areas of non-retail business in the town (INDUS), and other variables.

---

Step 1:

 

In the first step, we are going to import all the important libraries and most importantly, we have to import the dataset from sklearn.datasets.

---

from sklearn.linear_model import LinearRegression

from sklearn.datasets import load_boston

from sklearn.model_selection import train_test_split

import pandas as pd

import numpy as np

import matplotlib.pyplot as plt

boston = load_boston()

boston.data.shape, boston.target.shape

---

  

 The shape of the dataset 

---

Step 2

 

We are going to visualize the dataset with the help of a python library called pandas, we will name features of the dataset and afterward, we are going to create a data frame with the help of the pandas' library.

 

boston.feature_names

---

                                                           Feature names for the dataset

---

bos = pd.DataFrame(boston.data)

bos.columns = boston.feature_names

print(bos.head())

---

Visualization of the dataset using the pandas library

 

---

Step 3

 

In this step, we are going to split the dataset into training and test sets.

 

X_train, X_test, y_train, y_test = train_test_split(boston.data, boston.target, test_size=0.2)

print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)

 

The shape of the Training and Test set after Splitting

---

Step 4

 

Now, we are going to fit our dataset to another machine learning library from sklearn to implement linear regression.

sklinreg = LinearRegression(normalize=True)

sklinreg.fit(X_train, y_train)

 

---

Step 5

 

In the last step, we are printing test results on our dataset.

print("Train:", sklinreg.score(X_train, y_train))

print("Test:", sklinreg.score(X_test, y_test))

 

---

Training and testing accuracy

---

Logistic Regression

 

It is an algorithm that can be used for regression as well as classification tasks but it is widely used for classification tasks. The response variable that is binary belongs either to one of the classes. It is used to predict categorical variables with the help of dependent variables. 

 

Consider there are two classes and a new data point is to be checked which class it would belong to. Then algorithms compute probability values that range from 0 and 1. 

 

For example, whether it will rain today or not. In logistic regression weighted sum of input is passed through the sigmoid activation function and the curve which is obtained is called the sigmoid curve.

---

 

The figure shows a graph of Sigmoid Function

---

The logistic function that is a sigmoid function is an ‘S’ shaped curve that takes any real values and converts them between 0 to 1. If the output given by a sigmoid function is more than 0.5, the output is classified as 1 & if is less than 0.5, the output is classified as 0. If the graph goes to a negative end then y predicted will be 0 and vice versa.

 

If we obtain the output of sigmoid to be 0.75 then it tells us that there are 75% chances of that happening, maybe a toss coin.

 

---

    Binary Classification

---

The above figure shows inputs and the probabilities that the outcome is between two categories of a binary dependent variable based on one or more independent variables that can be continuous as well as categorical.

 

 Like the way, we implemented Linear Regression with the help of sklearn, Now, we shall implement Logistic Regression 

---

Step 1

 

import numpy as np

import matplotlib.pyplot as plt

import seaborn as sns

from sklearn.linear_model import LogisticRegression as SKLR

 

---

Step 2

 

1. Creating dataset with 1000 rows and 2 columns

2. Plotting the dataset with the help of the matplotlib library.

 

mean_01 = [0,0]

cov_01 = [[2,0.2], [0.2,1]]

mean_02 = [3,1]

cov_02 = [[1.5,-0.2], [-0.2,2]]

dist_01 = np.random.multivariate_normal(mean_01, cov_01, 500)

dist_02 = np.random.multivariate_normal(mean_02, cov_02, 500)

print(dist_01.shape, dist_02.shape)

Printed the shape of distributions

---

plt.figure()

plt.scatter(dist_01[:,0], dist_01[:,1], color='red')

plt.scatter(dist_02[:,0], dist_02[:,1], color='green')

plt.show()

 

---

Visualizing Dataset using Matplotlib

---

Step 3

 

dataset = np.zeros((dist_01.shape[0] + dist_02.shape[0], dist_01.shape[1] + 1))

dataset[:dist_01.shape[0], :-1] = dist_01

dataset[dist_01.shape[0]:, :-1] = dist_02

 

# Red = 0, Green = 1

dataset[dist_02.shape[0]:, -1] = 1

 

dataset.shape

---

The shape of the dataset

---

1. Adding both distributions, here, ‘1’ is added because of label column

2. Distributed first 500 data points to the first distribution

3. Distributed later 500 data points to the second distribution

4. Made a separate column for labels.

---

Step 4

 

np.random.shuffle(dataset)

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(dataset[:,:-1], dataset[:,-1], test_size=0.2)

X_train.shape, X_test.shape, y_train.shape, y_test.shape

The shape of Training and Testing Set after Splitting

---

1. Shuffled the dataset so that both distributions get mixed up properly so that they act as real-world problem dataset

2. Split dataset for the training set and test set

3. The visualized shape of the dataset

 

---

Step 5

 

In this step, we will fit our dataset to logistic regression with the help of sklearn.

 

sk_logreg = SKLR()

sklinreg.fit(X_train, y_train)

---

Fitted Logistic Regression to our Dataset

sk_logreg.score(X_test, y_test)

---

Output: 0.905

 

We have calculated our score for the test set and got a good accuracy of 90%.

 

Differences Between Linear And Logistic Regression

 

• Linear regression is used for predicting the continuous dependent variable using a given set of independent features whereas Logistic Regression is used to predict the categorical.

• Linear regression is used to solve regression problems whereas logistic regression is used to solve classification problems.

• In Linear regression, the approach is to find the best fit line to predict the output whereas in the Logistic regression approach is to try for S curved graphs that classify between the two classes that are 0 and 1.

• The method for accuracy in linear regression is the least square estimation whereas for logistic regression it is maximum likelihood estimation. 

• In Linear regression, the output should be continuous like price & age, whereas in Logistic regression the output must be categorical like either Yes / No or 0/1.

• There should be a linear relationship between the dependent and independent features in the case of Linear regression whereas it is not in the case of Logistic regression.

• There can be collinearity between independent features in the case of linear regression but it is not in the case of logistic regression.

 

 

Conclusion

 

In this blog, I have tried to give you a brief idea about how linear and logistic regression is different from each other with a hands-on problem statement. I have discussed the linear model, how sigmoid functions work, and how classification in logistic regression is made between 0 and 1. How prediction is made for continuous values. I have taken two problem statements where I have worked on classification as well as a regression problem. And lastly, I have discussed the differences between both the algorithms.